研究人員
研究群介紹
(1) MapReduce 程式的自動驗證與生成
程式語言與形式方法實驗室發展保證程式正確性之技術。我們在程式語言方面的研究,著重於發展正確程式之語法、語意、及實務上之議題;在形式方法方面的研究,強調分析真實程式中演算法、計算、以及實際方面之課題。我們應用數學及形式技術以探討我們的研究問題,亦致力於發展工具及方法論以幫助程式開發者寫作正確程式。
MapReduce 是很流行的資料平行運算模型。在MapReduce中,reducer 讀取一個串列的資料並產生對應的輸出。由於各平台排程策略不同,reducer 的輸入可能在每次執行時以不同順序抵達,因而產生了「reducer 可交換性問題」:reducer 的輸出和輸入到達的順序是否無關?我們證明了此問題在輸入的資料為數學整數時,是無法被決定的。然而,當輸入的資料型態為有限整數( 例如,電腦中的64 位元整數) 時,此問題是可被決定的。我們開發了名為「有理數暫存器自動機」的模型來表述reducer 程式。該模型有許多良好的數學性質,例如,相等和可交換性問題可在多項式空間內被解答。我們計劃以此模型作為reducer 程式自動生成的基礎。

(2) 低階密碼程式之正規驗證
現代密碼學仰賴大有限體上之計算。常見之計算設備卻不支援長整數(如255 位元)計算。因此,大有限體上之計算必須藉由32 或是64 位元指令來實現,而這些實現必然隨著計算結構不同而有所改變。在OpenSSL 中,大有限體乘法已經有x86、ARM、SPARC 上之實現。這些低階組合程式是否正確地被實現,在密碼學上非常重要。我們著重於發展實用的低階密碼程式形式化驗證技術。藉由與密碼專家之合作,我們的技術已經被用於驗證安全橢圓曲線Curve25519 群運算中的Montegory Ladderstep。
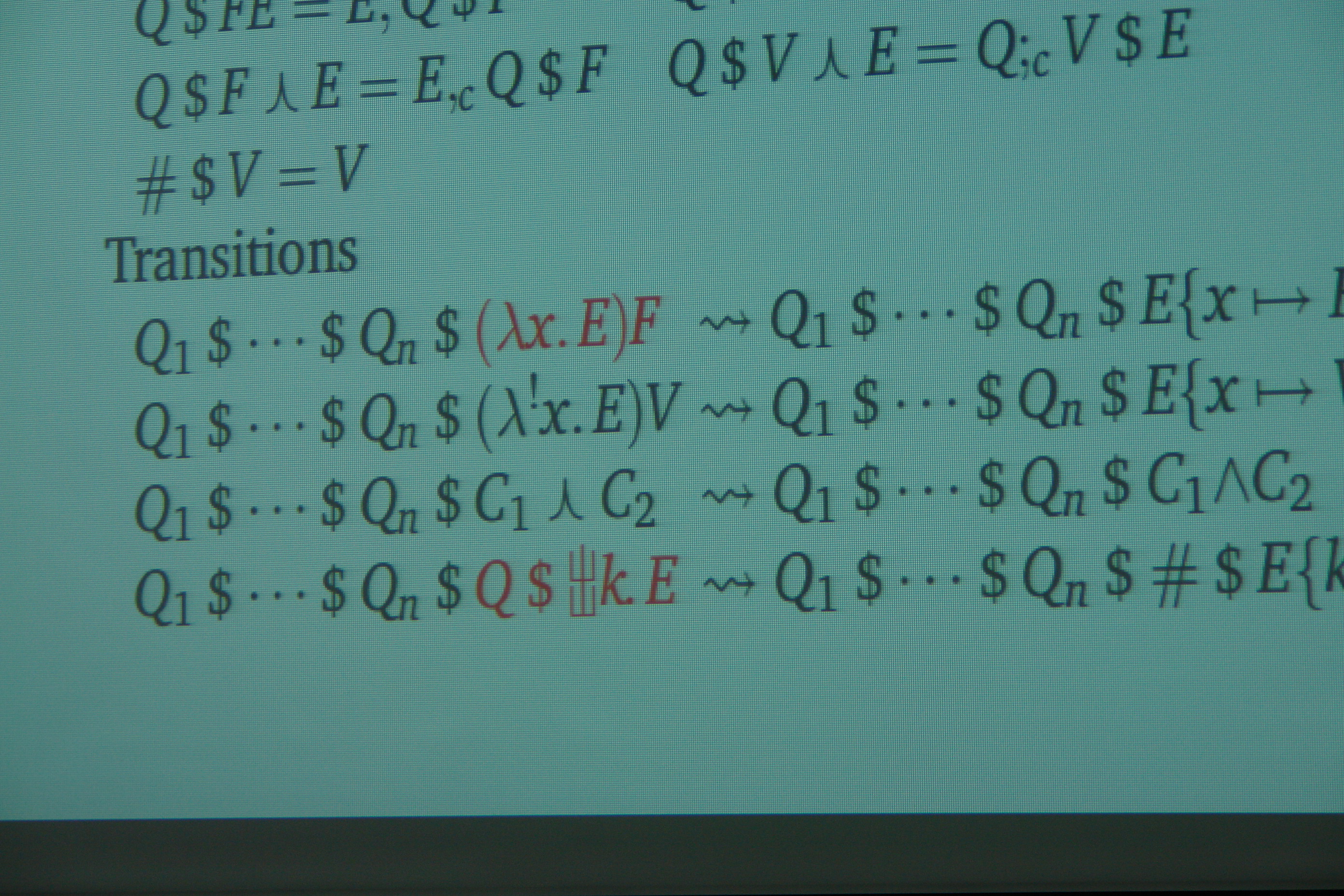
(3) 函數程式語言驗證與推導
函數程式語言提供一個單純、多限制的計算模型,但相對地,我們也因此擁有數學的好處:程式可當作數學來理解,可用包括歸納法在內的種種數學工具推論關於程式的性質。可從一個簡單、好理解、但作為程式執行效率不高的程式開始,用數學方法推導出一個和它「相等」,但執行效率高的程式。這套技巧稱作「程式推導」。我們做過幾個有趣的演算法推導,包括近似演算法、串列上的演算法等等。日後也將繼續尋找更多的程式推導例子,並建立推導程式的常用定理與步驟。一般的印象是函數語言中不允許副作用的存在。事實上,許多實用的函數語言不僅支援副作用,甚至支援許多種副作用。只是在函數語言中,我們會希望在支援副作用的同時不能失去函數語言原有的好處:副作用也須以嚴謹、能以數學方法管理的方式出現在程式中。其中一種管理、描述副作用的方式是透過「單子」。我們近年來也研究如何證明單子程式的性質,並嘗試釐清確保多種副作用結合後仍保持其應有性質的充分條件。
(4) 敏感資料之群組共享
隱私保護的意涵不僅在於個人資料取得上的限制,同時也在於資訊使用與揭露的原則與規範。妥善管理資訊流向、鼓勵資料分享、並維持所分享資訊的私密性,可真是挑戰。一般作法是透過集中式的資料控制單位,將來自眾多個人的資料集去識別化後,再行釋出供二次使用。不過,這三方——資料控制單位、個人、以及第三方資料使用者——的切身利益並不一致,這也是資料分享與再次使用的中心難題。經由與法律學者的合作,我們正發展以社群為出發的個人資料管理方式:在沒有外部的控制單位之下,社群成員間可以匯集關於自身的敏感,為共同的利益,供彼此使用。來自程式語言與形式方法的原則,將有助於我們發展可被驗證的、具良好性質的資料共享方式。我們將發展方法、工具、與系統,以實際幫助群體管理敏感資料。

(5) 教育、推廣
除了我們的研究活動外,我們同時也奉獻顯著的資源於教育。為了介紹我們的研究給學生,我們自2007 年以來,每年舉辦「台灣邏輯,語言和計算暑期學校 (FLOLAC)」。藉由 FLOLAC,鼓勵越來越多的台灣學生至程式語言和形式方法此一領域,學習並進行研究。

