Principal Investigators
Group Profile
The Programming Languages and Formal Methods research group develops techniques for ensuring program correctness. Our research into programming languages focuses on syntactic, semantic, and pragmatic issues in the development of correct programs. Our work on formal methods emphasizes the algorithmic, computational, and practical aspects of the analysis of realistic programs. We apply mathematical and formal techniques to the investigation of our research problems. We also aim to develop tools and methodologies to help developers in writing correct codes.(1) Verification and Synthesis of MapReduce Programs
MapReduce is a popular programming model for dataparallel computation, wherein the reducer produces an output from a list of inputs. Due to the scheduling policy of the platform, inputs may arrive at the reducers in various orders. The commutativity problem of reducers asks if the output of a reducer is independent of the input order. We proved that the problem is undecidable if the input is a list of mathematical integers, however, the problem becomes decidable if the inputs are bounded integers (the integers in computers). We also developed an automaton model for reducers, named register automata over rationals. The model has many good mathematical properties. For example, equivalence and commutativity problems can be decided in polynomial space. We plan to use the model as a basis for automatic code generation of reducers.

(2) Formal Verification on Low-Level Cryptographic Programs
Modern cryptography relies on computation over large finite fields. However, commodity computing devices do not natively support long (255-bit) integer computation. Therefore, computation over large finite fields must be implemented with 32- or 64-bit instructions. These implementations necessarily vary depending on the architecture. In OpenSSL, multiplication over large finite fields has been implemented for x86, ARM and SPARC. Whether all low-level assembly programs implement multiplication correctly is of utmost importance in cryptography. We focus on developing practical formal techniques for verifying functional properties on low-level cryptographic programs. In collaboration with practical cryptoanalysts, our technique has been applied to verify the Montgomery Ladderstep for the group operation on the secure elliptic curve Curve25519.
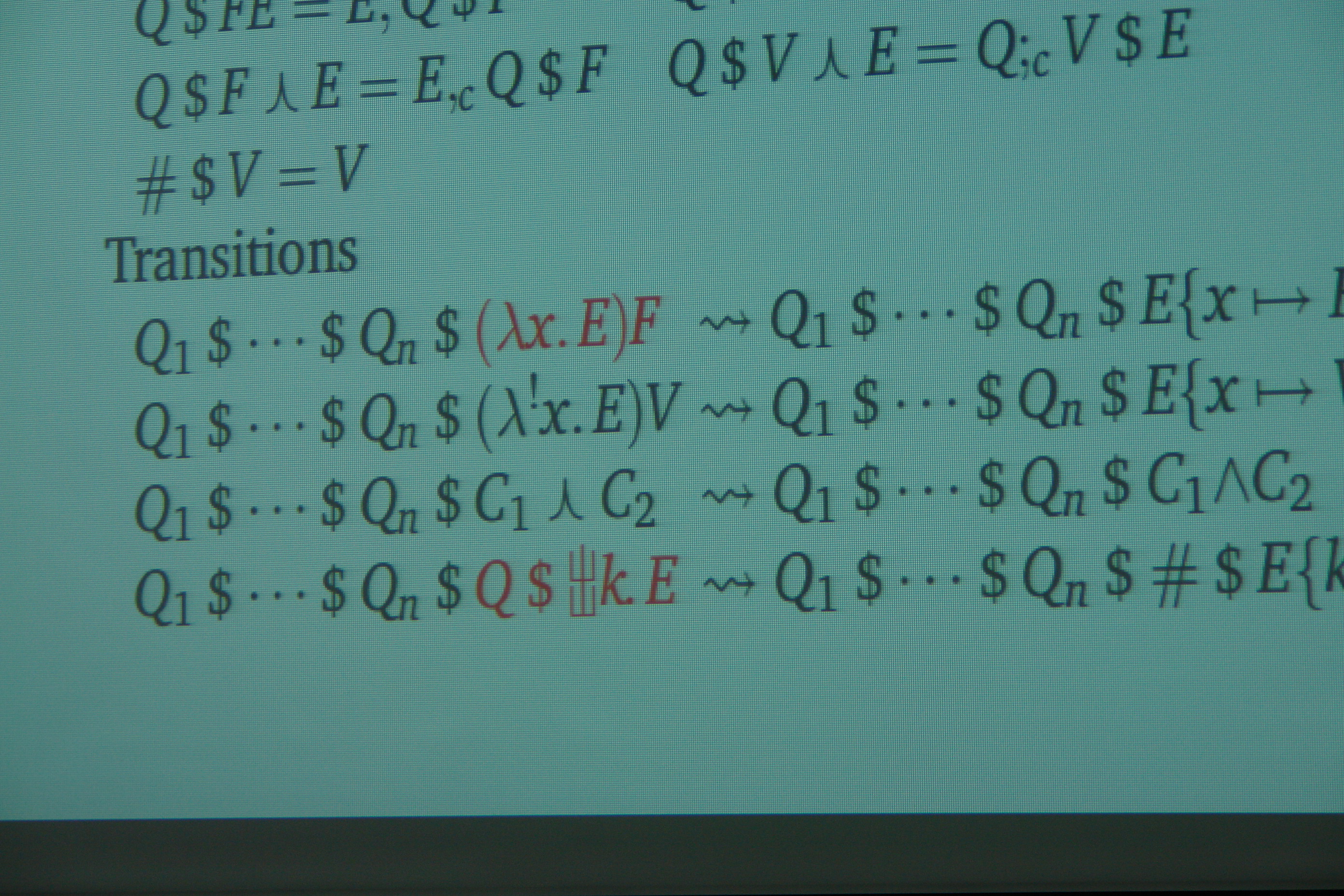
(3) Reasoning and Derivation of Functional and Monadic Programs
Purely functional languages, in which functions are true mathematical functions, offer a simple model of computation, where programs can be understood as mathematical equations whose properties can be proved using mathematical tools, such as induction. One can derive, from a program specification, an efficient program by stepwise equational reasoning, in which every step is justified by some theorem. This technique, called “program derivation”, aims to provide formalization and patterns that help programmers to develop programs and correctness proofs at the same time. We have published some interesting case studies of derivation, including approximation algorithms and algorithms for segment and partition problems. The general impression that purely functional languages do not allow side effects is misleading. Instead, these languages simply require that effects must be introduced in a mathematically manageable manner. One of the ways to introduce effects is through monads. Perhaps surprisingly, much reasoning can be performed with monadic programs. We are studying their derivation, and also trying to find conditions under which desired properties of one monadic effect can be preserved in presence of other monadic effects.

(4) Communal Sharing of Sensitive Data
Privacy refers not merely to restrictions on acquiring personal data, but also to a set of principles and rules that govern the use of information and disclosure. It remains a challenge to appropriately manage the flows of information such that data sharing is encouraged, while the shared information is kept private. A usual approach is for a centralized data controller to de-identify the dataset that was collected from individuals, before it is released for reuse. A central dilemma in this practice is that the three actors (individuals, data controllers, and third-party data users) often do not have their interests properly aligned. Together with legal scholars, we are working toward a communal approach to personal data management where, without an external authority, members of a community pool sensitive information about themselves for mutual benefit. Principles from programming languages and formal methods will guide us in the development of good data sharing schemes with verifiable properties. Methods, tools, and systems to facilitate communal management of sensitive data will be developed and put into use.

(5) Education
In addition to our research activities, we also dedicate significant resources to education. To introduce our research to students, we have organized the yearly Formosan Summer School on Logic, Language, and Computation (FLOLAC) since 2007. Through FLOLAC, many students in Taiwan have been encouraged to study and conduct research on programming languages and formal methods.

